Here are my notes on Q-learning and Q-transformer. Take it with grain of salt, as I am new in this area.
The Q-transformer is important paper, because it describes successful application of suboptimal synthetic (autonomously collected) data and transformer architecture in a robotic reinforcement learning problem.
Before Q-transformer let’s first talk about a bigger topic: Bellman Update in Reinforcement Learning.
States, Actions, and Rewards
Let’s suppose we have a game with game-states and rewarded actions we can take at each game-state. For example, in chess this is a state of the chessboard and actions are allowed moves we can make. Or for example, a Mario and Luigi computer game.
In chess, the reward is served only at the end, and the opponent may behave randomly. In Mario and Luigi instead, we collect coin rewards cumulatively throughout the game play, and the world is mostly rule-based.
In cases where the game world deterministic and the decision maker is in full control, we call the games Deterministic Sequential Decision Problems or Optimal Control Problems. In cases, where randomness impacts outcome of the decisions, and decision maker is not in a full control this problem called Markov Decision Process.
Let’s focus on Deterministic Sequential Decision Problems.
Example 1
Or even simpler example is below, where we have just a single state, single possible action, and single reward for that action.
In this diagram if we keep looping, we will keep stacking rewards. If we discount future rewards with 0.5 discount factor the total reward will be 2, so value of the state is 2.
Example 2
More interesting examples is where we have 2 possible actions:
In this case, we if we’re making the right decision, we still get reward 2, so the value of the state is still 2.
Example 3
But the above example demonstrates the discount factor importance, but is still a bit confusing because of the infinite possible paths. Let’s look at this 3 state example:
Can you see what is the best path in above?
Again, the best path is always choosing the first action.
With discount_factor=0.5 the value of the state 1 is:
value[state1] = 1 + 0.5 * 1 = 1.5
How do I know that? Well, working backwards from the last state. From State2 the best reward is through action1, and then again through action1. This solution approach is called Backward induction. Notice that Backward Induction has some similarities to Dijkstra’s shortest path algorithm in that we memorize the best paths to certain sub-set of states.
Bellman Equation
Optimal decision maker is always able to get the best in each situation in the total. Because the rewards are added to the total value, we can decompose the value of the state into the best action reward and the value of the next state.
The Principle of Optimality simply says that for the best decision maker (policy), no matter where you start or what your first step is, the next steps should always form the best plan for the situation after that first step. Where the best plan is the highest total reward. This principle is captured by the Bellman Equation, which is a necessary condition for optimality.
# Bellman Equation
value(current_state) == (
reward(current_state, the_best_action)
+ discount * value(the_best_next_state)
)
We can see this decomposition in the Example 3. We can also see, how Backward Induction solves the equation.
Notice the best next state, which is determined by maximizing the total value. We use maximum function here, which makes Bellman Equation non-linear.
Bellman Update
We can explore paths through states and actions and estimate minimal value as the total path reward starting from that state. Every time we find a better path, we can use the Bellman equation above to update the state value. This we iterate until we learn the best decision for every starting state.
From above, we can see that we can apply the principle of optimality above as an update rule to refine our decision-making, based on the trajectories we explored. We do this with Bellman Update.
We explore a different path or different action state and update corresponding value function with the action that leads along the path that leads to the highest reward. In many scenarios we will over time get to (converge) to the accurate value function.
Since we are storing values for each state, we represent the value function as an array or python dictionary:
# Bellman Update
value[current_state] = (
reward[current_state, the_best_action]
+ discount * value[the_best_next_state]
)
Value-iteration Method
Value-iteration method can be high-level described as:
- Determine or estimate initial each state value and action rewards.
- Based on the current value estimates, select optimal action in each state.
- Update the value of each state locally consistent with Bellman Update.
- Go to step 2.
There is also, Policy-iteration method, which focuses on finding policy rather than value function.
I read that the Value-interation method is a Fixed-Point Method and is likely to converge under reasonable conditions.
Q-function
Instead of a value function, it is easier to work with a Q-function. It is defined as follows:
# Bellman Equation with q_function
q_function[current_state, the_best_action] = (
reward[current_state, the_best_action]
+ discount * max(
q_function[the_best_next_state, the_next_action]
for the_next_action actions[the_best_next_state]
)
)
Q-function directly incorporates the total reward for each action we can take, so it informs us what is the best action.
With that we can describe the Bellman update rule in more detail:
states = [...] # list of all states
actions = [...] # list of all actions
gamma = 0.9 # discount factor
# The Q-table is initially filled with zeros
q_function = { (state, action): 0 for state in actions for action in actions }
def bellman_optimal_operator_update(q_function, state, action):
# this defined by the environment
next_state = get_next_state(state, action)
# the next action of in the next step as defined by the optiomal policy maximizing the q_function
# we directly update the q_function
q_function[state, action] = (
reward(state, action)
+ gamma * max(q_function[next_state, next_action] for next_action in actions)
)
return q_function
def optimal_policy(q_function, state):
# optimal policy is defined by action maximizing the q_function
return argmax(lambda a: q_function[a, state], all_actions(state))
Modelling Q-Function and Training It
Instead of model-free tabulation of the q-function, which is very memory-intensive, we can approximate the Q-function to interpolate the table using less than full data. In other words, we approximate the q-function with machine learning.
Temporal difference learning (TD-learning) is related to value-iteration or Q-learning, but it makes fewer assumptions about the environment. The method is called temporal difference because of the difference between current estimate, and one-lookahead estimate based on future state Q-function values.
Monte Carlo Return: A Q-Function Learning Speedup
At initialization, the neural model has a cold-start problem and is very bad at estimating the state values. But if we tabulate (memoize) rewards for successful trajectories, we can immediately provide a minimal reward for any point on the successful pathway. This speeds up learning of the Q-function neural network. This tabulation method is called Monte Carlo return. In a way, we are combing brute-force with neural network interpolation.
This is one of the tricks used in Q-Transformer.
Q-Transformer Paper Robotic State-Action-Reward Space
States consists of textual instruction, 320 × 256 camera image, robot arm position, robot arm orientation, robot arm gripper.
Actions consists of 8 dimensions: 3D position, 3D orientation, gripper closure command, and episode termination command.
Reward is received only at the end and the termination command must be triggered for policy to receive a positive reward upon task completion.
Q-Transformer Q-Function Learning
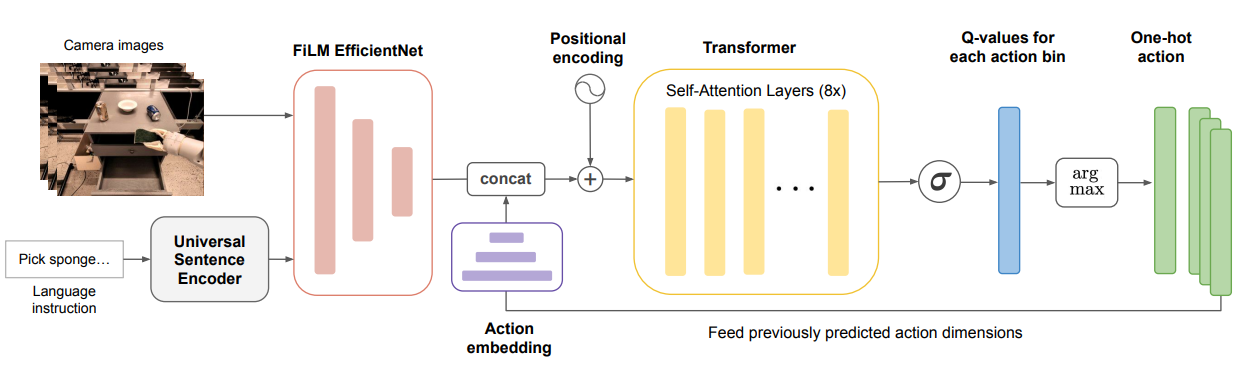
For example, in the Q-transformer a multi-modal neural network with transformer architecture is used for modeling the Q-function and TD-learning is used for offline training.
More specifically the input camera image goes to instruction-conditioned convolutional network for images. The text instruction conditions FiLM-conditioned visual-modality EfficientNet convolutional network. The conditioned network outputs a combined output information into a transformer, which then outputs Q-function value predictions.
Tricks used in Q-Transformer
The most foundational ideas applied in Q-transformer paper were described above. Here is a summary of other contributions in this paper:
-
Monte Carlo return: A method described above to reduce cold-start problem.
-
Autoregressive Discretization of Actions: To accommodate the high-capacity Transformer architecture, the Q-Transformer discretizes each dimension of the continuous action space separately and treats each dimension as a different timestep in the learning process. This allows the model to learn Q-values for each action dimension separately, enabling efficient scaling of the method to high-dimensional action spaces without encountering the curse of dimensionality.
-
Conservative Q-Function Regularization: The Q-Transformer uses a modified version of Conservative Q-learning (CQL) that introduces a regularizer to minimize Q-values for actions not present in the dataset explicitly. This conservative approach biases the model towards in-distribution actions, i.e., those seen during training, and serves to mitigate overestimation of Q-values for unseen or suboptimal actions. This approach ensures that during training, the estimated Q-values are kept closer to the minimal possible cumulative reward, which is consistent with the non-negative nature of the rewards in the tasks targeted by the Q-Transformer. This method differs from softmax method of pushing Q-values down for unobserved actions and up for the observed actions, which may prevent keeping Q-values low for suboptimal in-distribution actions that fail to achieve high reward.
-
Loss Function: The loss function for the Q-Transformer combines both the temporal difference error (between the current and target Q-values) and the conservative regularization term. The action space dimensionality is expanded to include the discrete bins of action values, and the update rule is applied separately for each action dimension.
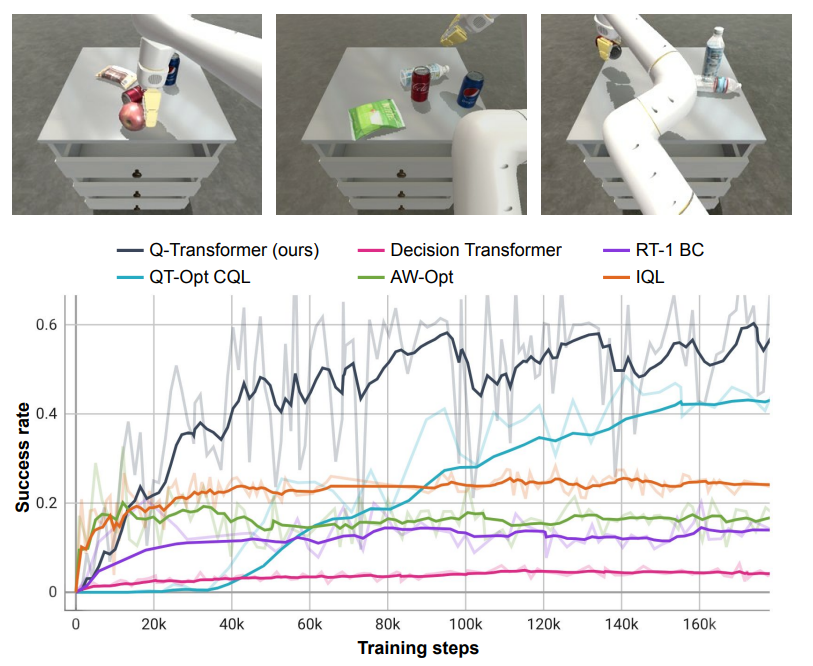
Q-Transformer Results
Q-Transformer outperforms QT-OPT and Decision Transformer in a reinforcement learning task, where suboptimal synthetic data is available for offline training. QT-OPT, also performs TD-learning in contrast to Decision Transformer, which seems to be the biggest factor here for good performance with suboptimal data.